Μαθηματικά Θέματα
Περιεχόμενα

Παίζοντας με τον Πυθαγόρα.
Ο Διόφαντος θεωρείται ο πρώτος "αλγεβρίστας" του κόσμου. Πράγματι η θεωρία των Διοφαντικών εξισώσεων στα τρία διασωθέντα βιβλία του, αποδεικνύει ότι η Άλγεβρα προϋπήρξε των Αράβων των Κινέζων και των Ινδών. Η άλγεβρα του Διόφαντου ασχολείται με εξισώσεις μιας ή περισσοτέρων μεταβλητών, που έχουν λύση στο σύνολο των ακεραίων αριθμών. Δηλαδή οι αριθμοί που θα βάλουμε στη θέση των αγνώστων \(x,y,z\), κλπ και που θα ικανοποιούν την εξίσωση πρέπει να είναι ακέραιοι.
Μια τέτοια είναι κι η πολύ γνωστή εξίσωση \[x^n+y^n=z^n,\] για την οποία ξόδεψαν τεράστιο χρόνο ενασχόλησης οι μαθηματικοί σε όλο τον κόσμο για να αποδείξουν αν για \(n \ge 3\), υπάρχουν ή όχι, ακέραιοι αριθμοί που να την επιλύουν.
Το 1996 ο Andrew Wiles μετά από πολλά χρόνια μυστικής έρευνας απέδειξε ότι δεν έχει λύσεις η εξίσωση αυτή για \(n \ge 3\). Βασικό του εργαλείο η θεωρία ελλειπτικών καμπυλών.
Ως γνωστό, για \(n=2\) έχουμε την εξίσωση που διέπει τα ορθογώνια τρίγωνα, το γνωστό θεώρημα του Πυθαγόρα. Για την συγκεκριμμένη εξίσωση υπάρχουν άπειρες λύσεις στους ακέραιους αριθμούς. Μια βασική λύση είναι η \(3,4,5\) όπου οι δυο πρώτοι αριθμοί είναι τα μήκη των καθέτων πλευρών ενός ορθογωνίου τριγώνου και ο τρίτος είναι το μήκος της υποτείνουσας του.
Το γιατί είναι άπειρες οι ακέραιες λύσεις της \(x^2+y^2=z^2\), είναι πολύ απλό, αφού αν πολλαπλασιάσουμε τα στοιχεία της τριάδας \(3,4,5\) με οποιονδήποτε ακέραιο, θα πάρουμε πάλι Πυθαγόρεια τριάδα αριθμών.
Αυτή η τριάδα που παράγει με έναν απλό πολλαπλασιασμό με ακέραιο, άλλες τριάδες ονομάζεται πρωτογενής. Η έρευνα λοιπόν και το ενδιαφέρον για Πυθαγόρειες τριάδες ασχολείται με την εύρεση των πρωτογενών τριάδων.
Παρουσιάζει ενδιαφέρον η εύρεση των πρωτογενών τριάδων, ζήτημα που απασχόλησε τους αρχαίους Έλληνες. Ήδη από την εποχή εκείνη ήταν γνωστή η μέθοδος εύρεσης των τριάδων αυτών για τους Πυθαγόρα, Ευκλείδη, Διόφαντο και άλλους.
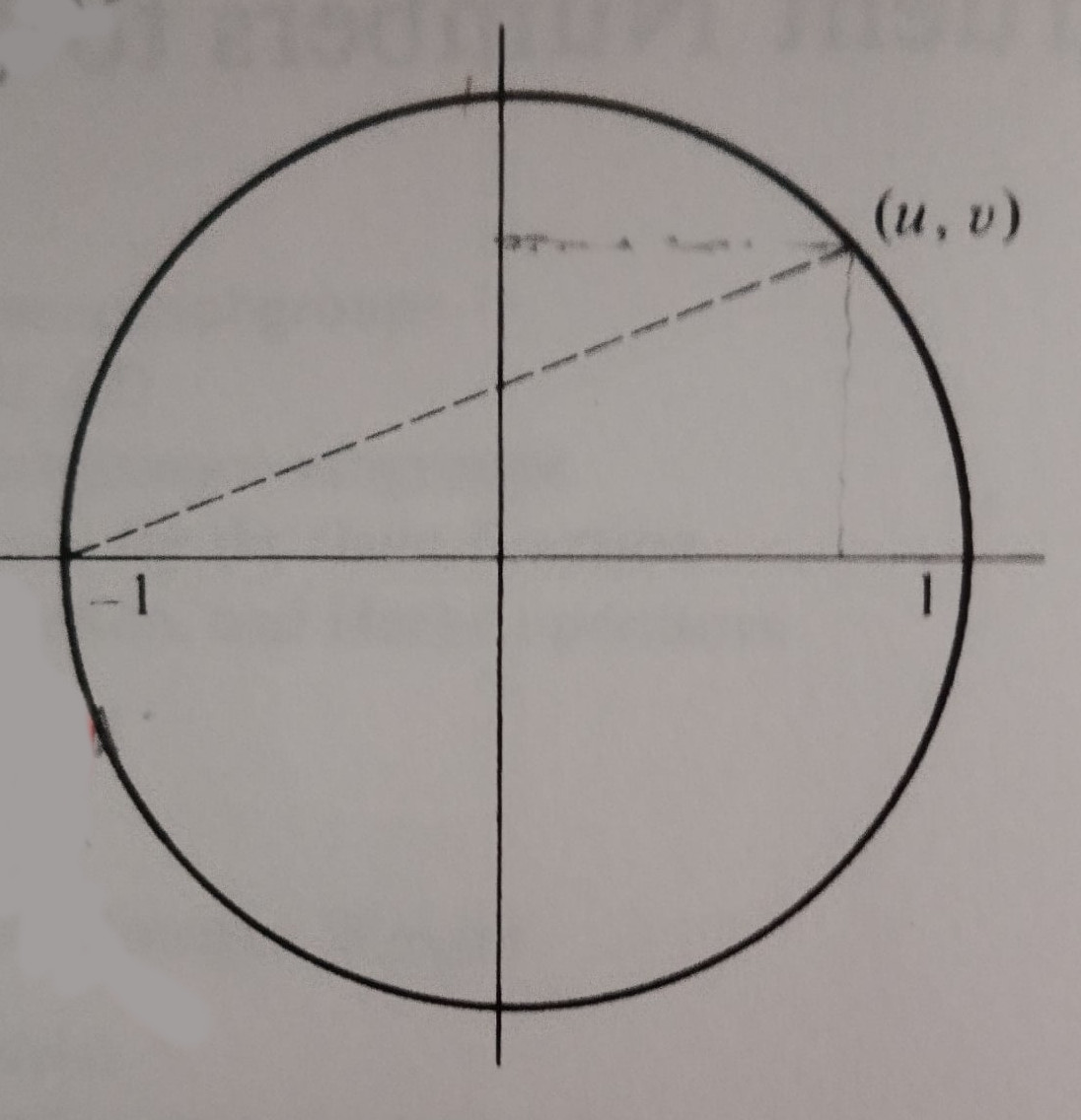
Σύμφωνα με την απλή αυτή μέθοδο, παίρνουμε δυό θετικούς ακέραιους \(a, b\) με \(a >b\), και \((a,b)=1\) και φέρνουμε την ευθεία γραμμή από το σημείο \((-1,0)\) με κλίση \(b/a\), που τέμνει τον μοναδιαίο κύκλο κέντρου \((0,0)\), στο σημείο \((u,v)\). Είναι εύκολο να δείξουμε ότι \[u=\frac{a^2-b^2}{a^2+b^2},\quad v=\frac{2ab}{a^2+b^2}.\] Είναι προφανές ότι οι ακέραιοι \(x=a^2-b^2, y=2ab, z=a^2+b^2\) αποτελούν μια Πυθαγόρεια τριάδα, αφού \(u^2+v^2=1.\) (Σχήμα 1.)
Οι πρωτογενείς Πυθαγόρειες τριάδες έχουν μέγιστο κοινό διαιρέτη το \(1\), είναι δηλαδή οι αριθμοί των τριάδων αυτών, πρώτοι προς αλλήλους, όπως λέμε στα μαθηματικά.
Βλέπουμε λοιπόν ότι βάζοντας θετικούς ακέραιους σαν τιμές των \(a\) και \(b\) που είναι πρώτοι προς αλλήλους, στις παραπάνω εξισώσεις, παίρνουμε όλες τις δυνατές πρωτογενείς Πυθαγόρειες τριάδες.